EE 212 Lab
Lab 5: Power Factor Correction
Prelab 5
Recall that average power absorbed by a circuit element is
VrmsIrmscos(θ-φ) where θ-φ is the phase
difference between the element's sinusoidal voltage v(t) and current
i(t). To obtain the most efficient use of the current delivered to a
load, it is desired that the load voltage and current be in phase
(θ-φ = 0, PF = 1) such that average power is maximized. The purpose
of this lab is to add compensation to an inductive load such that its
equivalent power factor becomes close to 1.
Notes on Measurements:
- Experimental determination of the power factor typically requires
the measurement of the phase difference between voltage and current.
Two properties of the function generator and oscilloscope make this
measurement difficult.
-
The reference (ground) leads on the oscilloscope and function generator
are internally tied to ground making it imperative that they all be
connected to the same point in the circuit.
- The difference between channels 1 and 2 (CH1-CH2) can only be displayed
by itself on the oscilloscope.
- Carefully consider where to take measurements such that subject to the above
constraints the information of interest can be determined.
Laboratory Procedure:
- Investigate inductive load
- An inductor is a coil of wire and wire has resistance. Measure the
resistance of your 0.47mH inductor. If this resistance is significant
include it your calculations.
- Construct the following circuit.
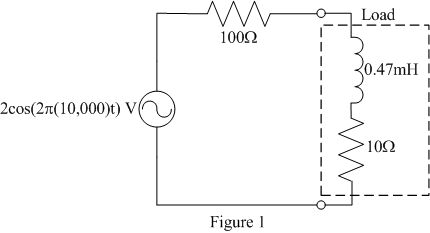
- Experimentally determine the load impedance ZL, power factor
angle θ-φ, power factor PF, and complex power using voltage and current
measurements. Compare these to your predicted values found in the prelab.
- Load power factor correction
- Add a capacitor of the value determined in the prelab in parallel with
the original load as shown in figure 2. Note the value of the capacitor
may need to be updated based upon the resistance of the inductor.
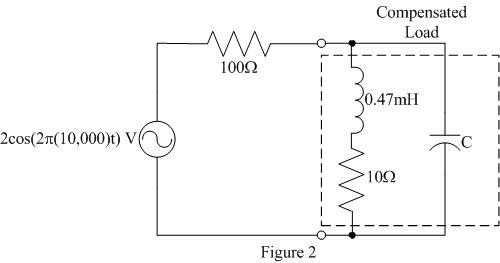
- Verify that your power factor correction is working. Due to the measurement
constraints described above, it might be easier to verify your power factor
correction by comparing the load voltage to the source voltage. What should
this relationship be and how does it compare to your experimental results?
- Normally, it isn't a good idea to change a circuit with input and power applied,
but carefully insert and remove the capacitor while watching the source and
load voltages to easily see the effect of the compensation.
- Does your load compensation work at other frequencies other than 10kHz?
Investigate this both mathematically and experimentally. Is there a
difference in the load as frequency is increased versus decreased?
© Copyright 2004 New Mexico Institute of Mining and Technology

