EE 212
Lab 10: Op-Amp Differentiators and Integrators
Prelab 10
Op-amp circuits are often designed
and implemented for signal differentiation and integration. Until recently
(before computer-based control), control algorithms (such as PID) containing
differentials and integrals were implemented in discrete circuit components.
Differentiation is also useful for obtaining velocity measurements from a signal
representing a position or determining a signal's frequency (recall the
amplitude of the time derivative of a sinusoid is scaled by its frequency).
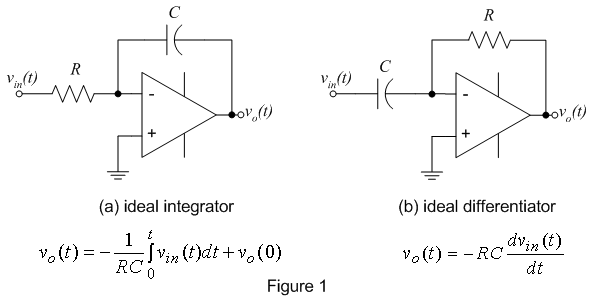
Figure 1 below shows an ideal op-amp integrator
and differentiator with input-output relationships that are theoretically
correct, but have practical implementation issues discussed below. In this lab,
practically realizable differentiators and integrators will be built using op-amps,
resistors and capacitors.
1. The Differentiator
- The ideal differentiator is inherently unstable in practice due to the
presence of some high frequency noise in every electronic system. An ideal differentiator would amplify
this small noise. For instance, if vnoise = Asin(ωt)
is differentiated, the output would be vout = Aωcos(ωt).
Even if A = 1μV, when ω = 2π(10MHz), vout would
have an amplitude of 63V! To circumvent this problem, it is traditional
to include a series resistor at the input and a parallel capacitor across
the feedback resistor as shown in figure 2, converting the differentiator to an integrator
at
high frequencies for filtering.
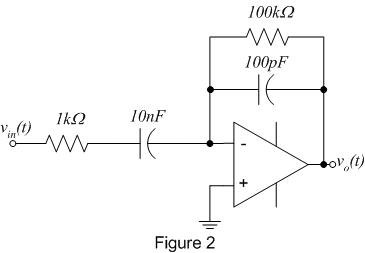
- Wire up the practical op-amp differentiator shown in figure 2 using your
op-amp of choice (741 or 356).
- Drive it (via vin(t)) with a 1kHz sine
wave, a 1kHz square wave, and a 1kHz triangle wave. For each input signal,
sketch the input and output waveforms.
- Are the output waveforms and their
amplitudes what you would expect, i.e., does the circuit differentiate the input
signal?
2. The Integrator
- Op-amps allow you to make nearly perfect integrators such as the practical
integrator shown in figure 3. The circuit incorporates a large resistor
in parallel with the feedback capacitor. This is necessary because real
op-amps have a small current flowing at their input terminals called the
"bias current". This current is typically a few nanoamps, and is neglected
in many circuits where the currents of interest are in the microamp to
milliamp range. However, if you apply a nanoamp current to a 0.1μF
capacitor, it won't take long until it charges and becomes effectively an
open circuit not allowing any current to flow! The feedback resistor gives
a path for the bias current to flow. The effect of the resistor on the
response is negligible at all but the lowest frequencies.
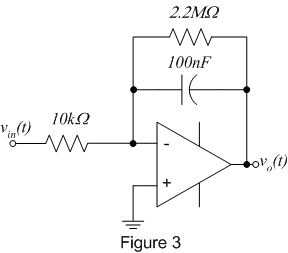
- Wire up the practical op-amp integrator shown in figure 3.
- Drive the input (via vin(t)) with a 500Hz square wave of 2 V
p-p amplitude. Sketch the input and output waveforms.
- Has the input been integrated?
- Calculate the expected
output waveform via integration using the circuit component values and compare
to the experimental waveform.
- Does the amplitude
of the output waveform agree with what it should be from the circuit values?
- Repeat using a sine wave and a triangle wave.
© Copyright 2003 New Mexico Institute of Mining and Technology



