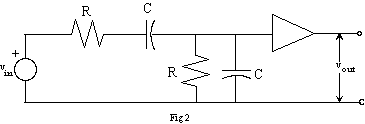
Connect the above circuit to a non-inverting amplifier based upon a 355/356 op-amp. This is depicted in figure 2 where its noted that the amplifier symbol (triangle) represents the non-inverting amplifier circuit. Adjust the gain of the amplifier and the frequency of the function generator until the amplitude and the phase of the output equal those of the input. (Include a precision (multi-turn) pot in the amplifier circuit to make the gain adjustable.)
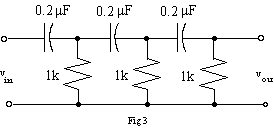
When the output is the same as the input, disconnect the signal generator and connect the output of the circuit to the input. With a little adjustment of the gain, the circuit should oscillate, producing a nice sine wave. Measure the frequency, and compare to the design frequency and the frequency measured in Part 1.
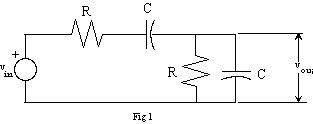
The RC network in Figure 3 can produce a phase shift of 180° at a desired frequency. In the prelab, you calculated this frequency for the component values given. Build the circuit. With a sinusoidal input, adjust the frequency of the function generator until the phase shift is 180°. Compare the frequency that yields 180° of phase to the frequency computed in the prelab. What is the gain of the circuit? How does this compare to your prelab result?
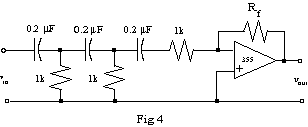
To make an oscillator, we need 0° or 360° of phase shift. Supply the extra phase shift with an inverting op-amp amplifier. The op-amp circuit can also supply the gain needed to make the input and output equal. Design and build the amplifier with adjustable gain. (The final 1 kW should become the input resistor, as it effectively goes to ground in both cases - compare Figure 3 and Figure 4.) Adjust the gain and frequency until vout = vin.
Complete the oscillator by again connecting the input to the output. Adjust the gain for an undistorted sine wave. Measure the frequency. How does this compare to the design frequency?