Solving equations with MATLAB

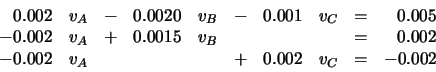
MATLAB is a computer program for doing numerical calculations. It is available on all the EE and TCC computers on campus. A Windows version of MATLAB is available to students to put on their personal computers - see your professor or Chris Langley to find out how to get this program. If you run Linux, Windows 95 or Windows NT on your computer there is a program called Octave which does most of the things MATLAB does, and will do all the analyses you need for this course. You can download Octave from http://www.che.wisc.edu/octave/octave.html.

To solve multiple equations using MATLAB (or Octave) write the equations with all the unkowns on the left hand side and the knowns on the right hand side: for example,


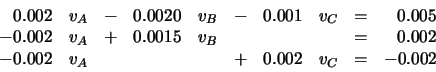
\begin{displaymath}\begin{array}{rrcrrcrrcr} 0.002 & v_A & - & 0.0020 & v_B & - ... ... -0.002 & v_A & & & & + & 0.002 & v_C & = & -0.002 \end{array}\end{displaymath}

To solve this equation in MATLAB type the folowing commands: 

A = [ 0.0020 -0.0020 -0.0010;
     -0.0020  0.0015  0.0000;
     -0.0020  0.0000  0.0020]

b = [ 0.005;
      0.005;
     -0.005]

v = A\b

The result will be 

v =

  6.4000 
  5.6000 
  2.2000

This means that vA = 6.4V, vB = 5.6V and vC = 2.2V.

Note: MATLAB will only solve numeric equations.

Suppose you had a set of equations which looked like this:


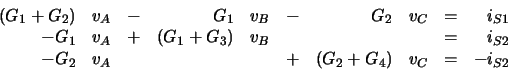
\begin{displaymath}\begin{array}{rrcrrcrrcr} (G_1 + G_2) & v_A & - & G_1 & v_B &... ...2 & v_A & & & & + & (G_2 + G_4) & v_C & = & -i_{S2} \end{array}\end{displaymath}

where R1 = 1k$\Omega$, R2 = 1k$\Omega$, R3 = 2k$\Omega$, R4 = 1k$\Omega$, iS1 = 5mA, and iS2 = 2mA. Then, to reduce the chance of error, you could let MATLAB find the coefficients before solving: 

G1 = 1/1e3;
G2 = 1/1e3;
G3 = 1/2e3;
G4 = 1/1e3;
i1 = 5e-3;
i2 = 2e-3;

A = [G1+G2 -G1     -G2;
     -G1    G1+G3    0;
     -G2    0      G2+G4]

b = [i1;
     i2;
     -i2]

v = A\b

The answer is 

v =

  6.4000
  5.6000
  2.2000

which means vA = 6.4V, vB = 5.6V and vC = 2.2V.


Bill Rison
1998-09-25