EE 451
Lab 5: FIR Filters and the 56002
- 1.
- The Fourier transform of a low-pass filter will have a value of 1 for
low frequencies and a value of 0 for high frequencies:
Let
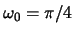 .
Find the impulse response of this discrete-time system by
taking the inverse Fourier transform of
.
Find the impulse response of this discrete-time system by
taking the inverse Fourier transform of
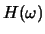 .
.
- 2.
- h[n] has an infinite number of terms, so cannot be implemented.
We can get an approximation of h[n] by taking a limited number of
terms. Take 101 terms of h[n], n = -50 ... +50. Print out
a stem plot of this truncated impulse response, h[n].
- 3.
- Take the Fourier transform of h[n]. Plot the
frequency response
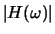 vs f and
vs f and
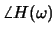 vs
f.
vs
f.
- 4.
- Implement the FIR filter on the 56002. The program fir.asm
is a macro to implement an FIR filter on the 56002, and the program
firt.asm shows how to use the macro. Note that when you call the fir macro, it expects the new input data x(n) to be in the x0
register, and when it exits, the new output data y(n) will be in the
a accumulator. You need to reserve storage in x data space
for the input data (states in the firt program), and need to
put the filter coefficients in the y data space (coef in the
firt program). Before you call the fir macro the first
time, you need to set up r0 to point at the input data array, r4 to point at the filter coefficients, and m0 and m4 to be
modulo the number of coefficients in the filter.
- 5.
- Measure the frequency response of the filter. Compare the
frequency response to the plots of Part 1.
- 6.
- This it a 100th order filter. What is the maximum order filter you
could implement on the 56002, keeping the 48 kHz sampling rate?
- 7.
- Use an audio CD to detemine the effect this filter has on music. How
different does the filtered music sound?



Next: About this document ...
Bill Rison
2000-09-22
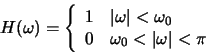
![]() .
Find the impulse response of this discrete-time system by
taking the inverse Fourier transform of
.
Find the impulse response of this discrete-time system by
taking the inverse Fourier transform of
![]() .
.
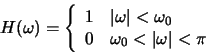
![]() .
Find the impulse response of this discrete-time system by
taking the inverse Fourier transform of
.
Find the impulse response of this discrete-time system by
taking the inverse Fourier transform of
![]() .
.