EE 451

Homework Assignment 5
Due Sept. 29, 2000

1.
Problem 4.9 (a) (d) (f)

2.
Problem 4.18

3.
The Fourier transform of a low-pass filter will have a value of 1 for low frequencies and a value of 0 for high frequencies:


\begin{displaymath}H(^{j\omega}) = \left\{ \begin{array}{ll}1 & \vert\omega\vert... ...\ 0 & \omega_0 < \vert\omega\vert < \pi \end{array} \right. \end{displaymath}

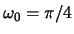Let $\omega_0 = \pi/4$.

(a)
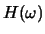Find the impulse response of this discrete-time system by taking the inverse Fourier transform of $H(e^{j\omega})$.

(b)
h[n] has an infinite number of terms, so cannot be implemented. We can get an approximation of h[n] by taking a limited number of terms. Take 101 terms of h[n], n = -50 ... +50. Print out a stem plot of this truncated impulse response, h[n].

(c)
Take the Fourier transform of h[n]. Plot the frequency response 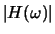$\vert H(e^{j\omega})\vert$ vs f and 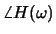$\angle H(e^{j\omega})$ vs f.


Bill Rison, <rison@ee.nmt.edu >
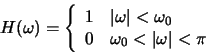
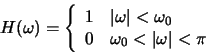