EE 451
Homework Assignment 8
Due Oct. 18, 2000
- Problem 5.21
- Problem 6.4. Note that the designer also needs some other chips (adders
and multipliers) to complete the job. You should just get an equation where
X(k) can be written in terms of three eight-point DFTs
X1(k), X2(k) and X3(k).
- Problem 6.11
- Let
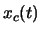 be a real-valued, bandlimited signal whose Fourier
transform
be a real-valued, bandlimited signal whose Fourier
transform 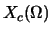 is zero for
is zero for
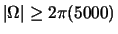 . The
sequence
. The
sequence 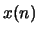 is obtained by sampling
is obtained by sampling 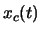 at 10 kHz. Assume that the
sequence
at 10 kHz. Assume that the
sequence 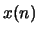 is zero for
is zero for 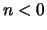 and
and 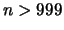 .
.
Let 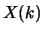 denote the 1000-point DFT of
denote the 1000-point DFT of 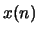 . It is known that
. It is known that 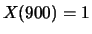 and
and 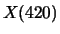 = 5. Determine
= 5. Determine 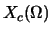 for as many values of
for as many values of 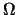 as
you can in the region
as
you can in the region
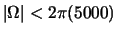 .
.
- Consider estimating the spectrum of a discrete-time signal
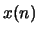 using
the DFT with a Hamming window for
using
the DFT with a Hamming window for 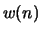 . A conservative rule of thumb for
the frequency resolution of windowed DFT analysis is that the frequency
resolution is equal to the width of the main lobe of
. A conservative rule of thumb for
the frequency resolution of windowed DFT analysis is that the frequency
resolution is equal to the width of the main lobe of 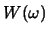 . You
wish to be able to resolve sinusoidal signals that are separated by as little
as
. You
wish to be able to resolve sinusoidal signals that are separated by as little
as 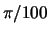 in
in 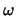 . In addition, your window length
. In addition, your window length 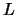 is constrained
to be a power of 2. What is the minimum length
is constrained
to be a power of 2. What is the minimum length 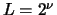 that will meet
your requirement?
that will meet
your requirement?
- Let
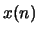 be a discrete-time signal whose spectrum you wish to estimate
using a windowed DFT. You are required to obtain a frequency resolution of at
least
be a discrete-time signal whose spectrum you wish to estimate
using a windowed DFT. You are required to obtain a frequency resolution of at
least 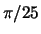 and are also required to use a window length
and are also required to use a window length 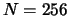 . A
safe estimate of the frequency resolution of a spectral estimate is the
main-lobe width of the window used. Which of the windows in Table 8.2 will
satisfy the criteria given for the desired frequency resolution?
. A
safe estimate of the frequency resolution of a spectral estimate is the
main-lobe width of the window used. Which of the windows in Table 8.2 will
satisfy the criteria given for the desired frequency resolution?
- Let
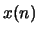 be a discrete-time signal obtained by sampling a
continuous-time signal
be a discrete-time signal obtained by sampling a
continuous-time signal 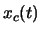 with some sampling period
with some sampling period 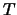 so the
so the
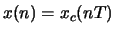 . Assume
. Assume 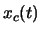 is bandlimited to 100 Hz, i.e.,
is bandlimited to 100 Hz, i.e.,
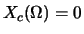 for
for
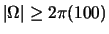 . We wish to estimate the continuous-time
spectrum
. We wish to estimate the continuous-time
spectrum 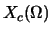 by computing a 1024-point DFT of
by computing a 1024-point DFT of 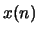 ,
, 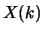 . What
is the smallest value of
. What
is the smallest value of 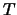 such that the equivalent frequency spacing
between consecutive DFT samples
such that the equivalent frequency spacing
between consecutive DFT samples 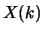 corresponds to 1 Hz or less in
continous time?
corresponds to 1 Hz or less in
continous time?
- Assume that
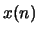 is a 1000-point sequence obtained by sampling a
continous-time signal,
is a 1000-point sequence obtained by sampling a
continous-time signal, 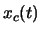 at 8 kHz and the
at 8 kHz and the 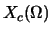 is sufficiently
bandlimited to avoid aliasing. What is the minimum DFT length
is sufficiently
bandlimited to avoid aliasing. What is the minimum DFT length 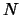 such that
adjacent samples of
such that
adjacent samples of 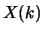 correspond to a frequency spacing of 5 Hz or less
in the original continuous-time signal?
correspond to a frequency spacing of 5 Hz or less
in the original continuous-time signal?
Note: Problems 4-8 are from Discrete-Time Signal Processing, 2nd Ed. by
Oppenheim and Schafer.
Bill Rison,
<rison@ee.nmt.edu >
![]() denote the 1000-point DFT of
denote the 1000-point DFT of ![]() . It is known that
. It is known that ![]() and
and ![]() = 5. Determine
= 5. Determine ![]() for as many values of
for as many values of ![]() as
you can in the region
as
you can in the region
![]() .
.
![]() denote the 1000-point DFT of
denote the 1000-point DFT of ![]() . It is known that
. It is known that ![]() and
and ![]() = 5. Determine
= 5. Determine ![]() for as many values of
for as many values of ![]() as
you can in the region
as
you can in the region
![]() .
.