- Take the inverse Fourier transform of
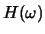 to show that:
to show that:
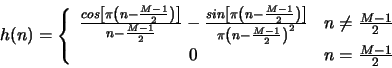
- Use the above equation with a Hamming window to find
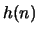 for a
differentiator where
for a
differentiator where 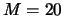 . Plot
. Plot 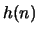 and plot the pole-zero diagram for
and plot the pole-zero diagram for 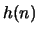 .
.
- Plot the gain
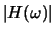 and phase
and phase
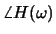 of the filter.
of the filter.
- In MATLAB, generate a signal
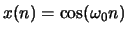 , where
, where
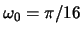 . Find 101 terms for
. Find 101 terms for 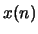 :
:
wo = pi/16; n = 0:100; x = cos(wo*n);Use the above
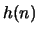 to filter the signal
to filter the signal 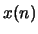 : y =
filter(h,1,x);. Use MATLAB to plot
: y =
filter(h,1,x);. Use MATLAB to plot 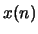 . Over the top of this, plot
. Over the top of this, plot
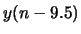 . (Remember that the output was delayed by
. (Remember that the output was delayed by 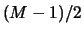 samples.)
Does
samples.)
Does 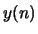 look like the derivative of
look like the derivative of 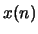 ?
?
- Repeat Part (e) for
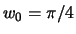 .
.
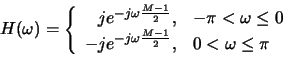
- Take the inverse Fourier transform of
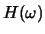 to show that:
to show that:
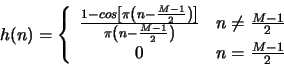
- Use the above equation with a Hamming window to find
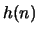 for a
Hilbert transformer where
for a
Hilbert transformer where 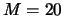 . Plot
. Plot 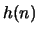 and plot the pole-zero diagram for
and plot the pole-zero diagram for 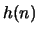 .
.
- Plot the gain
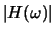 and phase
and phase
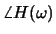 of the filter.
of the filter.
- In MATLAB, generate a signal
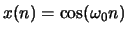 , where
, where
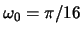 . Find 101 terms for
. Find 101 terms for 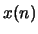 :
:
wo = pi/16; n = 0:100; x = cos(wo*n);Use the above
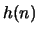 to filter the signal
to filter the signal 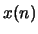 : y =
filter(h,1,x);. Use MATLAB to plot
: y =
filter(h,1,x);. Use MATLAB to plot 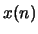 . Over the top of this, plot
. Over the top of this, plot
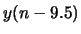 . (Remember that the output was delayed by
. (Remember that the output was delayed by 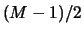 samples.)
Does
samples.)
Does 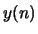 look like the ouput you would expect for a Hilbert transformer?
look like the ouput you would expect for a Hilbert transformer?
- Repeat Part (e) for
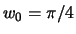 .
.