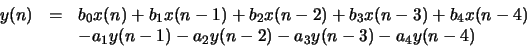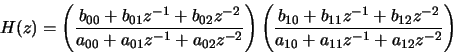EE 451
Lab 4: Digital Oscillators on the 56002
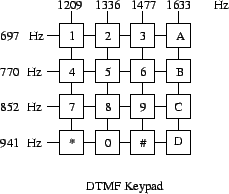
A touchtone telephone uses two frequencies for each key pressed. The
frequencies are shown in the diagram below:
Thus, when you press the ``1'' key you get a tone
where fL = 697 Hz and
fH = 1209 Hz.
These tones are called dual-tone multi-frequency (DTMF) signals.
In this lab we want to use the 56002 to generate these DTMF signals.
We can do this by implementing a
discrete-time system with an impulse response
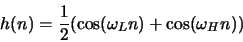 |
(1) |
This is a fourth-order system and can be written in the z-domain as
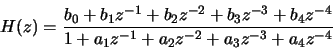 |
(2) |
This can be implemented in several ways. It can be implemented as a
fourth-order system by the difference equation:
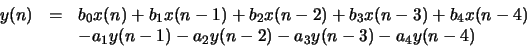 |
(3) |
It can be implemented as a cascade of second-order systems - in the
z-domain this would look like:
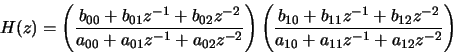 |
(4) |
It can be implemented in parallel form - in the z-domain this would look
like:
For reasons of stability in a finite word length processor the form in
Equation 5 is
the best for implementing this system.
- 1.
- Find the z-transform of Equation 1. Write it in the form of
Equation 5.
- 2.
- Write a MATLAB m-file which will calculate the ajk and bjkcoefficients when given the two frequencies
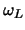 and
and 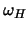 ,
and
will calculate the first few values of h1(n) and h2(n): h1(0),
h1(1), h1(2), h2(0), h2(1), and h2(2).
,
and
will calculate the first few values of h1(n) and h2(n): h1(0),
h1(1), h1(2), h2(0), h2(1), and h2(2).
Also, your MATLAB program should plot the impulse responses so you can see what
the signals should look like.
- 3.
- Run your MATLAB program to find the ajk's and initial values
needed for several different DTMF tones.
- 4.
- Write a program for the 56002 which will implement the difference
equation. Modify last week's lab to do this. Perhaps you can calculate
H1(z) in Accumulator a and H2(z) in Accumulator b,
and add the two together for the final result.
Note that your program needs no input. For n>2 the difference equation
for H1 is simply
h1(n) = -a11 h1(n-1) - a12 h1(n-2)
Thus, if you start your system at n = 3, with
h1(1) and h1(2) initialized in memory,
you do not need to use the bjk coefficients.
- 5.
- Test your program. Listen to the different outputs and see if they
sound like touch-tone tones. Look at the outputs on an oscilloscope
to determine if the two correct frequencies are present.
Bill Rison
2000-09-13