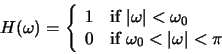
Consider a low-pass filter with the cutoff frequency
![]() .
Find the impulse response h(n) of this discrete-time system by taking the
inverse Fourier transform of H(w).
.
Find the impulse response h(n) of this discrete-time system by taking the
inverse Fourier transform of H(w).
Your filter uses 101 coefficients. It would be tedious and error-prone to type these coefficients into your program by hand. Instead, modify your MATLAB program to print the coefficients out for you in a way that they can automatically be included in your program. Here is a program fragment which can do this:
fid = fopen('lab4coef.asm','w');
fprintf(fid,'ntaps equ %d\n\n',length(h));
fprintf(fid,' org x:$100\n');
fprintf(fid,'states dsm ntaps\n\n');
fprintf(fid,' org y:0\n');
fprintf(fid,'coef\n');
for n=1:length(h)
fprintf(fid,' dc %14.8f\n',h(n));
end
fprintf(fid,'\n');
fclose(fid)
In your 56002 program the line
include lab4coef.asm
will put in the necessary information.