- (a)
-
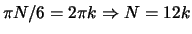 .
The smallest k for which
N is an integer is 1, so the period is N = 12
.
The smallest k for which
N is an integer is 1, so the period is N = 12 - (b)
-
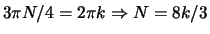 .
The smallest k for
which N is an integer is 3, so the perios is N = 8.
.
The smallest k for
which N is an integer is 3, so the perios is N = 8. - (c)
- This is not periodic.
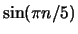 is periodic with period 10. When
you divide this by
is periodic with period 10. When
you divide this by 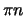 ,
it is no longer periodic - it gets smaller as n
gets bigger, so is not periodic.
,
it is no longer periodic - it gets smaller as n
gets bigger, so is not periodic.
n = -30:30; wo = pi/5; x = sin(wo*n)./(pi *n); x(n==0) = wo/pi; % L'Hospital's rule stem(n,x); grid title('x[n] = [sin(\pi n/5)]/(\pi n)'); ylabel('x[n]');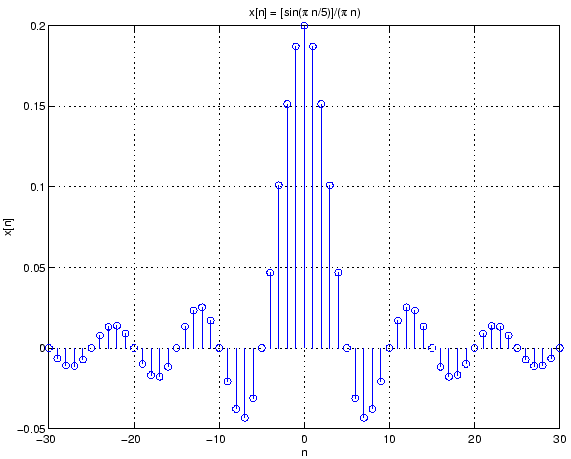
- (d)
-
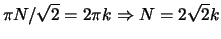 .
There is no
k which makes N an integer, so this is not periodic.
.
There is no
k which makes N an integer, so this is not periodic.
- (a)
n = -20:20; x = zeros(size(n)); x((n>=-1)&(n<=3)) = 1; x(n==4) = 1/2; subplot(321) stem(n,x) grid axis([-10 10 0 1.5]); title('x[n]'); subplot(322) na = n+2; stem(na,x); grid axis([-10 10 0 1.5]); title('x[n-2]'); subplot(323) nb = 4-n; stem(nb,x); grid axis([-10 10 0 1.5]); title('x[4-n]'); subplot(324) nc = -10:10; % x goes from -20:20, so y will go from -10:10 for k=-10:10 % (e.g., y[10] = x[20]) y(nc==k) = x(n==(2*k)); end stem(nc,y); grid axis([-10 10 0 1.5]); title('x[2n]'); subplot(325) y = x.*((2-n)>=0); stem(n,y); grid axis([-10 10 0 1.5]); title('x[n] u[2-n]'); subplot(326) ne = n+1; y = x.*(ne == 3); stem(ne,y); grid axis([-10 10 0 1.5]); title('x[n-1] \delta[n-3]');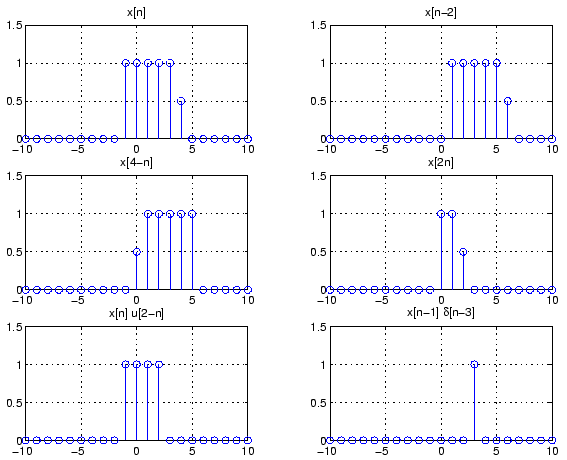
%(a)
subplot(311)
n=0:40;
x = (0.9).^n .* cos(0.1*pi*n+pi/5);
stem(n,x);
grid
ylabel('x[n]');
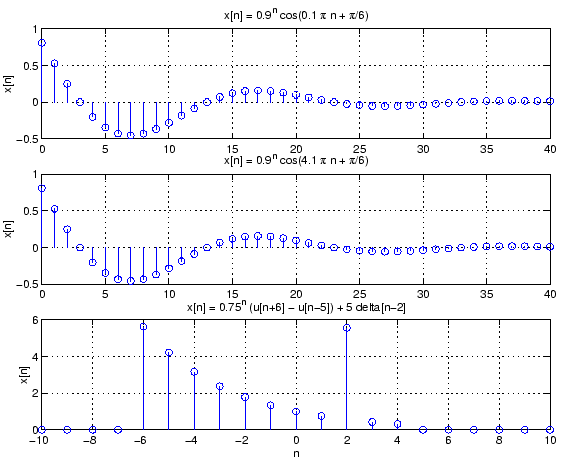
title('x[n] = 0.9^n cos(0.1 \pi n + \pi/6)');
%(b)
subplot(312)
n=0:40;
x = (0.9).^n .* cos(4.1*pi*n+pi/5);
stem(n,x);
grid
xlabel('n');
ylabel('x[n]');
title('x[n] = 0.9^n cos(4.1 \pi n + \pi/6)');
%(c)
subplot(313)
n=-10:10;
x=(0.75).^n .* (((n+6)>=0) - ((n-5)>=0)) + 5*(n==2);
stem(n,x);
grid
xlabel('n');
ylabel('x[n]');
title('x[n] = 0.75^n (u[n+6] - u[n-5]) + 5 delta[n-2]');
- (a)
- The system is not time invariant. Putting in a signal of 1 at time 0 will result in an output of 0. Putting in a signal of 1 at time 4 will result in an output of 4, so the same signal at different times gives different outputs.
- (b)
subplot(321) n = -20:20; x = (n>=0) - ((n-4)>=0); stem(n,x); grid axis([-10 10 -4 4]) title('x[n] = u[n] - u[n-4]');- (c)
subplot(322) y = n.*x; stem(n,y); grid axis([-10 10 -4 4]) title('y[n] = n x[n]');- (d)
subplot(323) stem(n+2,y) grid axis([-10 10 -4 4]) title('y[n-2]');- (e)
subplot(324) n1 = n+2; x1 = x; stem(n1,x1); grid axis([-10 10 -4 4]) grid title('x1[n] = x[n-2]');- (f)
subplot(325) y1 = n1.*x1; stem(n1,y1); grid axis([-10 10 -4 4]) grid title('y1[n]');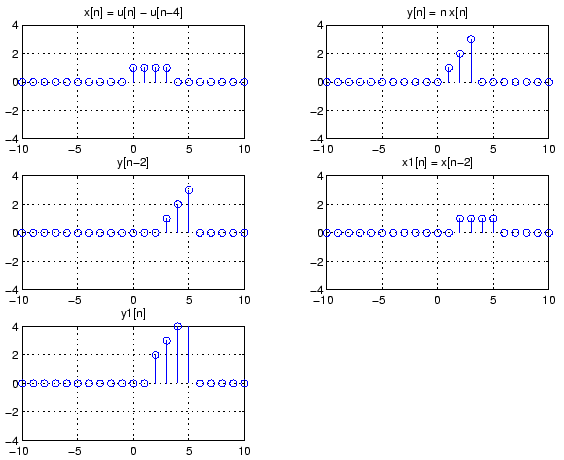
- (g)
-
![$y1[n] \ne y[n-2]$](img10.gif) .
.
- (a)
- The system is time invariant.
- (b)
subplot(321) n = -30:30; x = (n>=0) - ((n-4)>=0); stem(n,x); grid axis([-10 10 0 1.5]) title('x[n] = u[n] - u[n-4]');- (c)
subplot(322) ny=-15:15; for k=-15:15 y(ny==k) = (x((n+1)==k) + x(n==k) + x((n-1)==k))/3; end stem(ny,y); grid axis([-10 10 0 1.5]) title('y[n] = (x[n+1] + x[n] + x[n-1])/3');- (d)
subplot(323) stem(ny+2,y) grid axis([-10 10 0 1.5]) title('y[n-2]');- (e)
subplot(324) n1 = n+2; x1 = x; stem(n1,x1); grid axis([-10 10 0 1.5]) title('x1[n] = x[n-2]');- (f)
subplot(325) ny1 = -15:15; for k=-15:15 y1(ny1==k) = (x((n1+1)==k) + x(n1==k) + x((n1-1)==k))/3; end stem(ny1,y1); grid axis([-10 10 0 1.5]) title('y1[n]');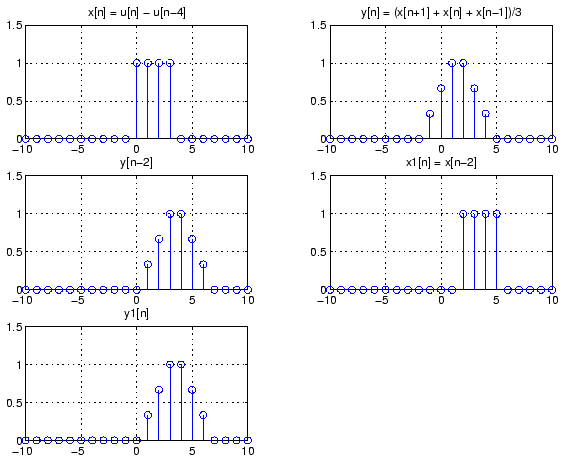
- (g)
-
y1[n] = y[n-2].