EE 451 - HW 4

Solutions

1.
Problem 3.1
(a)
Look up in table
(b)
Look up in table
(c)

\begin{displaymath}\left(\frac{1}{2}\right)^n u[-n] = \left(\frac{1}{2}\right)^n u[-n-1] + \delta(n) \end{displaymath}


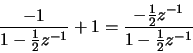
\begin{displaymath}\frac{-1}{1-\frac{1}{2}z^{-1}} + 1 = \frac{-\frac{1}{2}z^{-1}}{1-\frac{1}{2}z^{-1}} \end{displaymath}


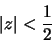
\begin{displaymath}\vert z\vert < \frac{1}{2}\end{displaymath}

(d)
Look up in table
(e)
Look up in table
(f)
Look up in table
(g)

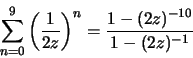
\begin{displaymath}\sum_{n=0}^{9}\left(\frac{1}{2z}\right)^n = \frac{1-(2z)^{-10}}{1-(2z)^{-1}} \end{displaymath}

Finite-length sequence, so converges everywhere.
2.
Problem 3.4
(a)
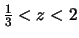If the Fourier transform exists, X(z) converges on the unit circle. Thus $\frac{1}{3} < z < 2$.
(b)
ROC of two-sided sequences must be a disk. The only possible disks are 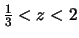$\frac{1}{3} < z < 2$ and 2 < z < 3. Thus, there are two possible two-sided sequences.
(c)
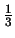No - ROC of stable sequences include the unit circle. For stable sequence the pole at $\frac{1}{3}$ is causal, but the poles at 2 and 3 are non-causal.
3.
Problem 3.7
(a)

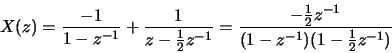
\begin{displaymath}X(z) = \frac{-1}{1-z^{-1}} + \frac{1}{z-\frac{1}{2}z^{-1}} = \frac{-\frac{1}{2}z^{-1}}{(1-z^{-1})(1-\frac{1}{2}z^{-1})} \end{displaymath}


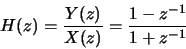
\begin{displaymath}H(z) = \frac{Y(z)}{X(z)} = \frac{1-z^{-1}}{1+z^{-1}}\end{displaymath}

(b)
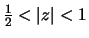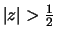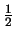The ROC of X(z) is $\frac{1}{2} < \vert z\vert < 1$. However the pole of X(z) which limits the ROC to be less than 1 is cancelled by the zero of H(z) (the u[-n-1] part of x[n] is cancelled), so the ROC of X(z) which remains is $\vert z\vert > \frac{1}{2}$. The ROC of Y(z) is the region which satifies the remaining constraint on X(z) (|z| > $\frac{1}{2}$) and the constraint on H(z) (|z| > 1). Thus, Y(z) converges on |z| > 1.
(c)

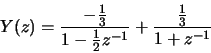
\begin{displaymath}Y(z) = \frac{-\frac{1}{3}}{1-\frac{1}{2}z^{-1}} + \frac{\frac{1}{3}}{1+z^{-1}} \end{displaymath}

with ROC |z| > 1, so both must be right-handed sequences. Thus,

\begin{displaymath}y[n] = -\frac{1}{3}\left(\frac{1}{2}\right)^n u[n] + \frac{1}{3}(-1)^n u[n]\end{displaymath}

4.
Problem 3.9
(a)

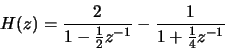
\begin{displaymath}H(z) = \frac{2}{1-\frac{1}{2}z^{-1}} - \frac{1}{1+\frac{1}{4}z^{-1}}\end{displaymath}

Since H(z) is causal, the ROC is outside all poles, so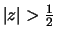 $\vert z\vert > \frac{1}{2}$.
(b)
The system is stable since the ROC contains the unit circle.
(c)

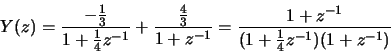
\begin{displaymath}Y(z) = \frac{-\frac{1}{3}}{1+\frac{1}{4}z^{-1}} + \frac{\frac... ...}{1+z^{-1}} = \frac{1+z^{-1}}{(1+\frac{1}{4}z^{-1})(1+z^{-1})} \end{displaymath}

The ROC is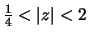 $\frac{1}{4} < \vert z\vert < 2$.

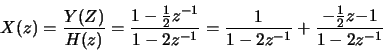
\begin{displaymath}X(z) = \frac{Y(Z)}{H(z)} = \frac{1-\frac{1}{2}z^{-1}}{1-2z^{-1}} = \frac{1}{1-2z^{-1}} + \frac{-\frac{1}{2}z{-1}}{1-2z^{-1}} \end{displaymath}

Since the intersection of the ROC of X(z) with the ROC of H(z) gives the ROC of Y(z), the ROC of X(z) must be |z| < 2, so the sequences are left-handed:

\begin{displaymath}x[n] = -(2)^nv[-n-1]+\frac{1}{2}(2)^{n-1}u[-n]\end{displaymath}

5.

\begin{displaymath}H(z) = \frac{2}{1-\frac{1}{2}z^{-1}} - \frac{1}{1+\frac{1}{4}z^{-1}}\end{displaymath}


\begin{displaymath}h[n] = 2\left(\frac{1}{2}\right)^nu[n] - \left(-\frac{1}{4}\right)^nu[n]\end{displaymath}

6.
Problem 3.10
(a)
Both are right-hand sequences, so ROC is outside largest pole 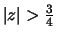$\vert z\vert > \frac{3}{4}$. The ROC includes the unit circle, so the Fourier transfrom converges.
(b)
Finite-length sequence so converges everywhere (except z=0). The ROC includes the unit circle, so the Fourier transfrom converges.
(c)
Left-hand sequence, so ROC is inside smallest pole |z| < 2. The ROC includes the unit circle, so the Fourier transfrom converges.
(d)
Both are right-hand sequences, so ROC is outside largest pole |z| > 1. The ROC does not include the unit circle, so the Fourier transfrom does not converge.
(e)
x[n] is finite-length sequence with only positive powers of z, so it converges everywhere. ROC contains unit circle, so Fourier transform converges.
(f)
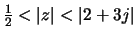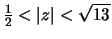ROC outside pole for right-hand sequence, and inside pole for left-hand sequence. Thus $\frac{1}{2} < \vert z\vert<\vert 2+3j\vert$, or $\frac{1}{2} < \vert z\vert < \sqrt{13}$. The ROC includes the unit circle, so the Fourier transfrom converges.
7.
Problem 3.16
(a)

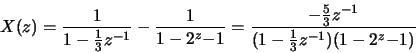
\begin{displaymath}X(z) = \frac{1}{1-\frac{1}{3}z^{-1}} - \frac{1}{1-2^z{-1}} = \frac{-\frac{5}{3}z^{-1}}{(1-\frac{1}{3}z^{-1})({1-2^z{-1}})} \end{displaymath}

The ROC is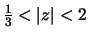 $\frac{1}{3}<\vert z\vert<2$

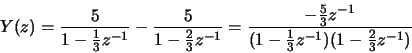
\begin{displaymath}Y(z) = \frac{5}{1-\frac{1}{3}z^{-1}}-\frac{5}{1-\frac{2}{3}z^... ...\frac{5}{3}z^{-1}}{(1-\frac{1}{3}z^{-1})(1-\frac{2}{3}z^{-1})} \end{displaymath}

The ROC is outside the largest pole, so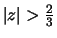 $\vert z\vert > \frac{2}{3}$.

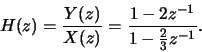
\begin{displaymath}H(z) = \frac{Y(z)}{X(z)} = \frac{1-2z^{-1}}{1-\frac{2}{3}z^{-1}}. \end{displaymath}

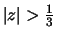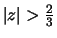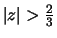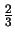The zero at 2 in H(z) cancels the pole at 2 in X(z), so the appropriate ROC for the left-over part of X(z) is $\vert z\vert > \frac{1}{3}$. The ROC of Y(z) is the intersection of the ROC of H(z) and the ROC of the left over part of X(z). Since the ROC of Y(z) is $\vert z\vert > \frac{2}{3}$, the ROC of H(z) must be $\vert z\vert > \frac{2}{3}$. The pole-zero plot of H(z) will have a pole at $\frac{2}{3}$ and a zero at 2.
(b)

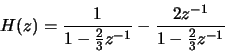
\begin{displaymath}H(z) = \frac{1}{1-\frac{2}{3}z^{-1}} - \frac{2z^{-1}}{1-\frac{2}{3}z^{-1}}\end{displaymath}


\begin{displaymath}h[n] = \left(\frac{2}{3}\right)^n u[n] - 2\left(\frac{2}{3}\right)^{n-1}u[n-1] = \left(\frac{2}{3}\right)^n(u[n]-3u[n-1])\end{displaymath}

(c)

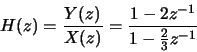
\begin{displaymath}H(z) = \frac{Y(z)}{X(z)} = \frac{1-2z^{-1}}{1-\frac{2}{3}z^{-1}}\end{displaymath}


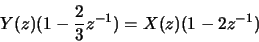
\begin{displaymath}Y(z)(1-\frac{2}{3}z^{-1}) = X(z)(1-2z^{-1})\end{displaymath}


\begin{displaymath}y[n] - \frac{2}{3}y[n-1] = x[n]-2x[n-1]\end{displaymath}

(d)
The ROC of H(z) contains the unit circle, so H(z) is stable.
8.
Problem 3.20
(a)
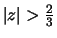The ROC of H(z) has to be chosen so that the ROC of Y(z) is the intersection of the ROC of H(z) and the ROC of X(z). Thus ROC of H(z)is $\vert z\vert > \frac{2}{3}$.
(b)

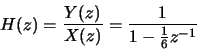
\begin{displaymath}H(z) = \frac{Y(z)}{X(z)} = \frac{1}{1-\frac{1}{6}z^{-1}}\end{displaymath}

ROC of H(z) is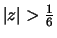 $\vert z\vert > \frac{1}{6}$.
9.
Problem 3.22
(a)

\begin{displaymath}h[n] = 3 \left(-\frac{1}{3}\right)^n i[n]\end{displaymath}


x[n] = u[n]


\begin{displaymath}y[n]=\sum_{n=-\infty}^{\infty}h[k]x[n-k]= \sum_{n=-\infty}^{\infty}\left(3{\left( -\frac{1}{3}\right)}^k u[k]\right)u[n-k] \end{displaymath}


\begin{displaymath}= \sum_{k=0}^{n}3\left(-\frac{1}{3}\right)^k = \frac{9}{4}\left(1-{\left(-\frac{1}{3}\right)}^{n+1}\right)u[n] \end{displaymath}

(b)

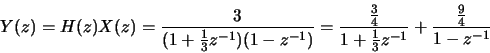
\begin{displaymath}Y(z) = H(z) X(z) = \frac{3}{(1+\frac{1}{3}z^{-1})(1-z^{-1})}=... ...{\frac{3}{4}}{1+\frac{1}{3}z^{-1}}+\frac{\frac{9}{4}}{1-z^{-1}}\end{displaymath}


\begin{displaymath}y[n] = \frac{3}{4}\left(-\frac{1}{3}\right)^nu[n] + \frac{9}{4}u[n]\end{displaymath}


\begin{displaymath}= \frac{9}{4}\left(1-{\left(-\frac{1}{3}\right)}^{n+1}\right)u[n] \end{displaymath}

10.
Problem 3.40
(a)

v[n] = x[n]-w[n] => V(z) = X(z) - W(z)

Let the output of the H(z) block be y[n]. Then

w[n] = e[n] + y[n] => W(z) = E(z) + Y(z) = E(z) + H(z) V(z)

Now eliminate V(z) between the above two equations:

W(z) = E(z) + H(z)(X(z)-W(z))


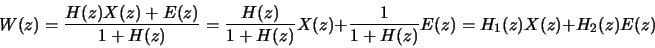
\begin{displaymath}W(z) = \frac{H(z)X(z)+E(z)}{1+H(z)} = \frac{H(z)}{1+H(z)}X(z) + \frac{1}{1+H(z)}E(z) = H_1(z) X(z) +H_2(z)E(z)\end{displaymath}

Thus, H1(z) = H(z)/(1+H(z)) and H2(z) = 1/(1+H(z)).
(b)

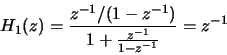
\begin{displaymath}H_1(z) = \frac{z^{-1}/(1-z^{-1})}{1+\frac{z^{-1}}{1-z^{-1}}} = z^{-1}\end{displaymath}

(c)

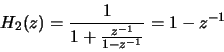
\begin{displaymath}H_2(z) = \frac{1}{1+\frac{z^{-1}}{1-z^{-1}}} = 1-z^{-1}\end{displaymath}

(d)
H(z) is not stable due to the pole at z=1. H1(z) and H2(z) are both stable (finite-length sequences are always stable).
11.
Problem 3.43
(a)

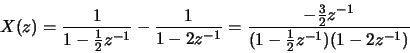
\begin{displaymath}X(z) = \frac{1}{1-\frac{1}{2}z^{-1}}-\frac{1}{1-2z^{-1}} = \frac{-\frac{3}{2}z^{-1}}{(1-\frac{1}{2}z^{-1})(1-2z^{-1})}\end{displaymath}

ROC of X(z) is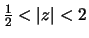 $\frac{1}{2} < \vert z\vert < 2$.

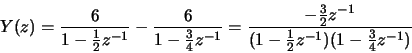
\begin{displaymath}Y(z) = \frac{6}{1-\frac{1}{2}z^{-1}}-\frac{6}{1-\frac{3}{4}z^... ...-\frac{3}{2}z^{-1}}{(1-\frac{1}{2}z^{-1})(1-\frac{3}{4}z^{-1})}\end{displaymath}

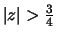ROC of Y(z) is $\vert z\vert > \frac{3}{4}$.

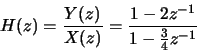
\begin{displaymath}H(z) = \frac{Y(z)}{X(z)} = \frac{1-2z^{-1}}{1-\frac{3}{4}z^{-1}}\end{displaymath}

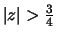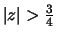ROC of H(z) is $\vert z\vert > \frac{3}{4}$. This will make sure ROC of Y(z) is $\vert z\vert > \frac{3}{4}$ (note that the zero of H(z) at z=2 cancels the pole of X(z) at z=2, so the ROC of Y(z) is not limited to the region |z| < 2).
(b)

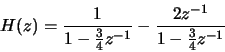
\begin{displaymath}H(z) = \frac{1}{1-\frac{3}{4}z^{-1}}- \frac{2 z^{-1}}{1-\frac{3}{4}z^{-1}}\end{displaymath}


\begin{displaymath}h[n] = \left(\frac{3}{4}\right)^nu[n]-2\left(\frac{3}{4}\right)^{n-1}u[n-1]\end{displaymath}

(c)

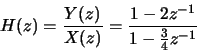
\begin{displaymath}H(z) = \frac{Y(z)}{X(z)} = \frac{1-2z^{-1}}{1-\frac{3}{4}z^{-1}}\end{displaymath}


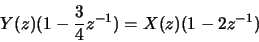
\begin{displaymath}Y(z)(1-\frac{3}{4}z^{-1}) = X(z)(1-2z^{-1})\end{displaymath}


\begin{displaymath}y[n] - \frac{3}{4}y[n-1] = x[n]-2x[n-1]\end{displaymath}

(d)
H(z) is stable since the ROC includes the unit circle. It is causal since h[n] = 0 for n < 0.


Bill Rison
1999-09-29