- First build and test the amplifier. Use a 10k pot for the feedback resistor R2 and choose R1 so that the gain K of the amplifier can be varied from 1 to 3. Sketch the amplifier schematic. This amplifier enable the pole locations to be varied at constant radius f0 from the negative real axis onto the j omega axis.
- Design and construct a single-stage filter having its poles at a radius f0 = 10 kHz. Set the gain for a Butterworth frequency response. This circuit will be tested with your function generator, which has a 50 ohms source impedance. The source impedance will be in series with the input resistor R of the filter, so you will need either to make R large in comparison, and/or to take the source impedance into account when constructing the circuit. NOTE: the resistors for the amplifier are not equal to each other or to the filter resistors.
- First test the amplifier by first measuring its low-frequency gain and comparing with what the gain should be.
- Confirm that the filter has a low-pass frequency response and measure its cutoff or 3-dB frequency fc. For a Butterworth filter, the 3-dB cutoff frequency should be the same as the pole radius, i.e., w0 = wc. Is it?
- Measure and plot the frequency response (measure and plot the gain at each kHz from about 1 to 15 kHz). Compare this with theory and Matlab plot form the prelab.
- Measure and document (carefully draw) the step response of the filter for comparison with later results. Does the step response overshoot? What is the gain after the transient response dies out, and what should the gain be?
- Sketch the pole locations of this filter, approximately to scale. Use the transfer function for this.
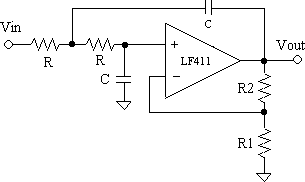
Don't change the R's and C's that determine fc.
- What are the effects of varying the amplifier gain and thus the pole locations on the step response of the filter?
- Document for the step response of a Bessel filter (K = 1.268). Compare this with the Matlab plot form the prelab.
- Document for the step response of a 2.0 dB Chebyshev filter (K = 2.114). Compare this with the Matlab plot form the prelab.
- Measure and plot the frequency response of the 2.0 dB Chebyshev filter (measure and plot the gain at each kHz from about 1 to 15 kHz). Compare this with theory and Matlab plot form the prelab.
- Observe the plot of the frequency response of the 2.0 dB Chebyshev filter. Why is it peaked? The peaking constitutes the `ripple' of the (frequency response of the) filter. Is the ripple equal to 2.0 dB? Measure the 3 dB cutoff frequency and compare with the theoretical value obtained from fn = 0.907. (fn = f0 / fc, f0 is determined by RC, and fc is the 3-dB frequency) Why is the cutoff frequency larger than the pole radius? Illustrate using a sketch of the pole locations similar to that of part 1. Compare this with the Matlab plot form the prelab.
- Measure and plot the frequency response and fn for the Bessel filter and compare with theory (measure and plot the gain at each kHz from about 1 to 15 kHz). Does the Bessel filter have ripple? Sketch its pole locations, as before. Compare this with the Matlab plot form the prelab.
- Compare the filters. Does the Butterworth filter have the flattest response? Which has the fastest falloff at high frequencies? Which has the best step response?