Prelab 10

The purpose of this lab is to experimentally construct the frequency responses of two circuits. The circuits to be studied are the passive RLC circuit shown in figure 1 and the active network shown in figure 2.

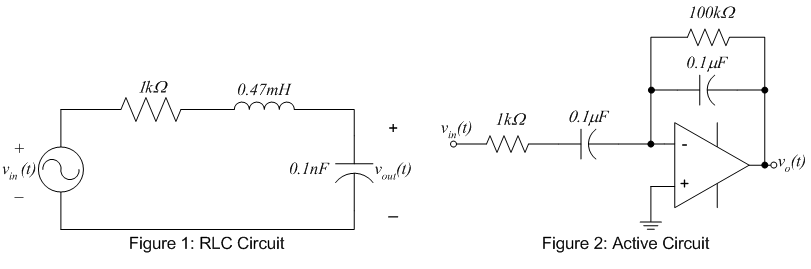
1. Frequency response of RLC circuit.

• Construct the circuit shown in figure 1.
• Let v_in(t) be a 1 V_p-p sine wave for which you'll vary the frequency. 
• Use your prelab results as a guide as to what frequency range should be used and measure the frequency response (magnitude and phase) of V_out(jw)/V_in (jw). Note the function generator and oscilloscope display frequency in Hertz and your Bode plots are likely versus frequency in rad/sec, so make sure to convert whichever way you choose to keep the units consistent. Take extra points in regions where the magnitude or phase change quickly.
• Compare your results with the calculated values plotted in the prelab by recording the experimental data on top of the calculated prelab data.
• How would one describe this circuit?
• Does this passive circuit ever yield a gain larger than 1 (0dB)? If so, how is this possible?

2. Frequency response of active circuit.

• Construct the circuit shown in figure 2.
• Let v_in(t) be a 1 V_p-p sine wave for which you'll vary the frequency. 
• Use your prelab results as a guide to what frequency range should be used and measure the frequency response (magnitude and phase) of V_out(jw)/ V_in (jw). Note the function generator and oscilloscope display frequency in Hertz and your Bode plot is likely versus frequency in rad/sec, so make sure to convert whichever way you choose to keep the units consistent. Take extra points in regions where the magnitude or phase change quickly.
• Compare your results with the calculated values plotted in the prelab by recording the experimental data on top of the calculated prelab data.
• How would one describe this circuit?