EE 212L: Frequency Response of Circuits

Objective: The purpose of this lab is to experimentally construct and verify the frequency responses of two circuits. The circuits to be studied are the passive RLC circuit shown in Figure 1 and the active network shown in Figure 2.

Pre-lab:

  1. Determine the transfer function Vo(jω)/Vi(jω) for the circuits shown in Figures 1 and 2 below.
  2. Plot the frequency responses (magnitude and phase using a computer-based tool such as Matlab) for these circuits keeping in mind:
    • linear and/or logarithmic axes may be used as may Decibels (dB), so choose which will be easiest to replicate and verify experimentally (i.e., you will be experimentally constructing these same plots);
    • ensure key regions are readily visable for meaningful comparison with experimental results; and
    • the frequency responses may be significantly affected by the internal resistance of the function generator and/or impedance of the oscillocope probe, so include their effects as warranted.

Laboratory Procedure:

  1. Frequency Response of an RLC Circuit
    • Construct the circuit shown in Figure 1.
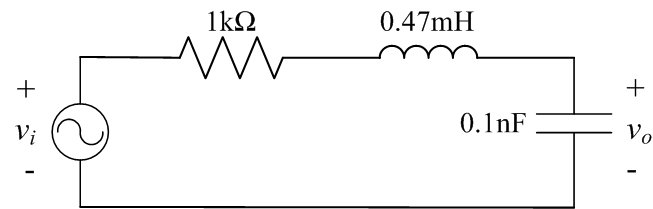
      Figure 1: Series RLC circuit
    • Let vi(t) be a 2 Vp-p sine wave for which you'll vary the frequency.
    • Use your prelab results as a guide as to what frequency range should be used and experimentally find (via measurements) a table of values for the frequency response (magnitude and phase) of Vo(jω)/Vi(jω). Note the function generator and oscilloscope display frequency in Hertz and your plots are likely versus frequency in rad/sec, so make sure to convert in whichever way you choose to keep the units consistent. Take extra points in regions where the magnitude or phase change quickly.
    • Compare your results with the calculated values plotted in the prelab by recording the experimental data on top of the calculated prelab data/plots.
    • How would one describe this circuit?
    • Does this passive circuit ever yield a gain larger than 1 (0dB)? If so, how is this possible?

  2. Frequency Response of an Active Circuit
    • Construct the circuit shown in Figure 2.
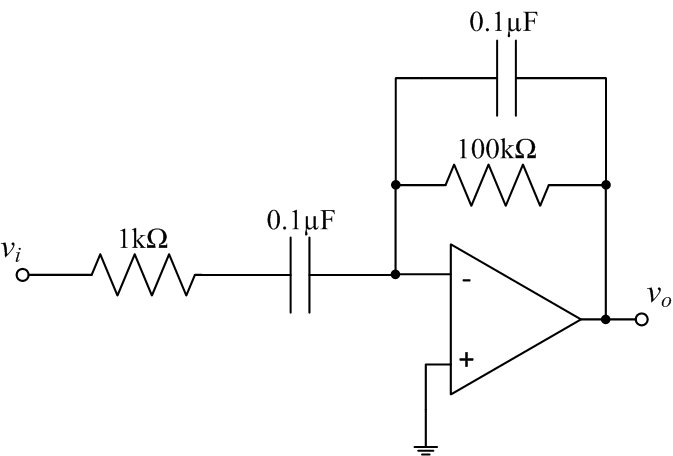
      Figure 2: Active (op-amp-based) circuit
    • Let vi(t) be a 2 Vp-p sine wave for which you'll vary the frequency.
    • Use your prelab results as a guide as to what frequency range should be used and experimentally find (via measurements) a table of values for the frequency response (magnitude and phase) of Vo(jω)/Vi(jω). Note the function generator and oscilloscope display frequency in Hertz and your plots are likely versus frequency in rad/sec, so make sure to convert in whichever way you choose to keep the units consistent. Take extra points in regions where the magnitude or phase change quickly.
    • Compare your results with the calculated values plotted in the prelab by recording the experimental data on top of the calculated prelab data/plots.
    • How would one describe this circuit?




© Copyright 2004 New Mexico Institute of Mining and Technology

Revised MAR2015