EE443: MATLAB DC MOTOR SIMULATION

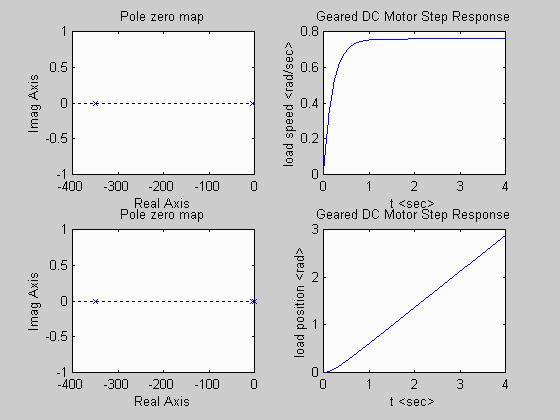
This example shows how MATLAB commands can be used to reduce the block diagram of a dc motor and then simulate its response for a 12V step input.

%
% Filename:  example1.m
%
% Description:  This m-file demonstrates how matlab can be
%               used to reduce the block diagram of a DC motor
%               with gearing and then simulate the motors
%               response to a 12V step input.

clear; clf;

% Motor parameters:
  Jm = 0.01; bm = 0.3; Km = 0.8;
  Kb = 0.8; R = 1.4; L = 0.004;

% Gear paramters:
  N1 = 10; N2 = 61;

% Load parameters:
  Jl = 11; bl = 27;

% Equivalent load seen by motor:
  Jt = Jm + (N1/N2)^2*Jl;
  bt = bm + (N1/N2)^2*bl;

% Determine Motor Transfer Function Omegal(s)/V_a(s):
  nume = [1]; dene = [L R];
  disp('Ia(s)/(Va(s)-Vb(s)) = '); printsys(nume,dene,'s');

  numm = [Km]; denm = [Jt bt];
  disp('Omega(s)/Ia(s) = '); printsys(numm,denm,'s');

  numg = [N1]; deng = [N2];
  disp('Omegal(s)/Omegam(s) = '); printsys(numg,deng,'s');

  numf = [Kb]; denf = [1];
  disp('Vb(s)/Omegam(s) = '); printsys(numf,denf,'s');

  [numser,denser] = series(nume,dene,numm,denm);
  [numfdbk,denfdbk] = feedback(numser,denser,numf,denf,-1);
  [numdtf,dendtf] = series(numfdbk,denfdbk,numg,deng);

  disp('Omegal(s)/Va(s) = '); printsys(numdtf,dendtf,'s');
  
% Determine and plot poles and zeros of speed system:
  subplot(2,2,1); pzmap(numdtf,dendtf);
  disp('zeros = '); roots(numdtf)
  disp('poles = '); roots(dendtf)

% Plot speed response of system to a 12V step input:
  t = 0:0.01:4;
  omegal = 12*step(numdtf, dendtf, t);
  subplot(2,2,2); plot(t,omegal);
  xlabel('t '); ylabel('load speed ');
  title('Geared DC Motor Step Response');

% Determine Motor Transfer Function Thetal(s)/V_a(s):
  [numtf,dentf] = series(numdtf,dendtf,[1],[1 0]);

% Determine and plot poles and zeros of position system:
  subplot(2,2,3); pzmap(numtf,dentf);
  disp('zeros = '); roots(numtf)
  disp('poles = '); roots(dentf)

% Plot position response of system to a 12V step input:
  thetal = 12*step(numtf, dentf, t);
  subplot(2,2,4); plot(t,thetal);
  xlabel('t '); ylabel('load position ');
  title('Geared DC Motor Step Response');

Ia(s)/(Va(s)-Vb(s)) = 
 
num/den = 
 
         1
   -------------
   0.004 s + 1.4
Omega(s)/Ia(s) = 
 
num/den = 
 
           0.8
   ------------------
   0.30562 s + 1.0256
Omegal(s)/Omegam(s) = 
 
num/den = 
 
   10
   --
   61
Vb(s)/Omegam(s) = 
 
num/den = 
 
   0.8
   ---
    1
Omegal(s)/Va(s) = 
 
num/den = 
 
                    8
   -----------------------------------
   0.074571 s^2 + 26.3502 s + 126.6272
zeros = 

ans =

   Empty matrix: 0-by-1

poles = 

ans =

 -348.4831
   -4.8728

zeros = 

ans =

   Empty matrix: 0-by-1

poles = 

ans =

         0
 -348.4831
   -4.8728