EE443: MATLAB PENDULUM SIMULATION

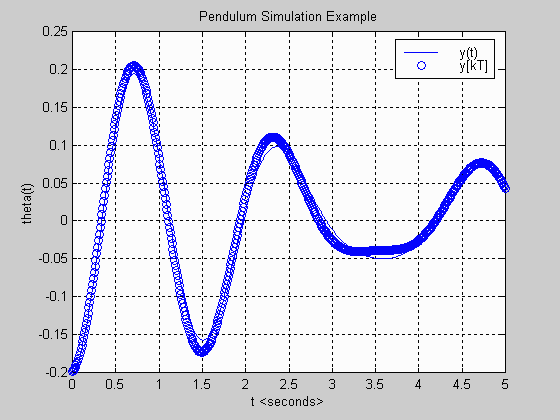
This example shows how MATLAB commands can be used to simulate a pendulum using the continuous-time and discrete-time state variable models.

%
% Filename: example2.m
%
% Description:  This m-file demonstrates how matlab can be used to compute
%               the discrete-time approximation to the solution of the 
%               pendulum state and output equations.  The input will be a
%               sinusoidal torque.
%

clear; clf;				% clear matlab memory and figure

m = 5.0; l = 0.5; g = 9.81; b = 1.3;    % define system parameters

A = [0 1; -g/l -b/(m*l*l)];		% define system state matrices
B = [0;1/(m*l*l)];
C = [1 0];
D = [0];

x0 = [-0.2; 0.1];			% initial conditions
tmax = 5;				% maximum time in simulation

[num,den] = ss2tf(A,B,C,D); 		% compute system transfer function
disp('Theta(s)/T(s) = ');
printsys(num,den,'s');
disp(' ');

disp('poles =');			% compute system poles
roots(den)
disp(' ');

disp('eigenvalues = ');			% compute system eigenvalues
eig(A)
disp(' ');

t = 0:0.01:tmax;			% perform 'cont-time' simulation
Torque = sin(pi*t);
[y,x] = lsim(A,B,C,D,Torque,t,x0);
plot(t,y); grid;
xlabel('t '); ylabel('theta(t)');
title('Pendulum Simulation Example');
hold;

xk = x0; T = 0.01;			% define initial conditions & time step

for k = 0:tmax/T,			% perform 'disc-time' simulation
   xk = (T*A + eye(2,2))*xk + T*B*sin(pi*k*T);
   yk = C*xk;
   plot(k*T,yk,'o');
end;
hold;

legend('y(t)', 'y[kT]');		% create a legend

Theta(s)/T(s) = 
 
num/den = 
 
            0.8
   --------------------
   s^2 + 1.04 s + 19.62
 
poles =

ans =

  -0.5200 + 4.3988i
  -0.5200 - 4.3988i

 
eigenvalues = 

ans =

  -0.5200 + 4.3988i
  -0.5200 - 4.3988i

 
Current plot held
Current plot released