EE443 Example 9: Dynamic State Variable Control
Matlab m-file:
%
% File Name: example9.m
%
% Description: M-file showing design and implementation of dynamic
% state variable controller.
%
clear ; clf ; % clear memory and figure
A = [0 1; -5 -8] ; % state matrices
B = [0; 2] ;
C = [1 1] ;
Acl = [0 C; 0 A(1,:); 0 A(2,:)] ; % closed-loop system w/error dynamics
Bcl = [0; B] ;
yd = 3.0 ; % desired output
dt = 0.001 ; % simulation time step
% Peform First State Feedback Design
K = acker(Acl, Bcl, [-2 -2 -20]) % determine feedback gains
x = [0; 0] ; y = C*x ; % initial conditions
inte = 0.0 ;
tvec = 0.0 ; yvec = 0.0 ; i = 1 ; % define vectors for storing outputs
for t = 0.0:dt:5.0, % loop over time for simulation
inte = inte + dt*(y - yd) ; % integral of output error
u = -K*[inte; x] ; % state controller
xdot = A*x + B*u ; % plant dynamics
x = xdot*dt + x ; % euler integrate dynamics
y = C*x ; % output equation
yvec(i) = y ; tvec(i) = t ; % store output & time into vectors
i = i + 1 ; % increment vector index
end ;
plot(tvec, yvec) ; % plot output with labels
xlabel('time (sec)') ; ylabel('y') ;
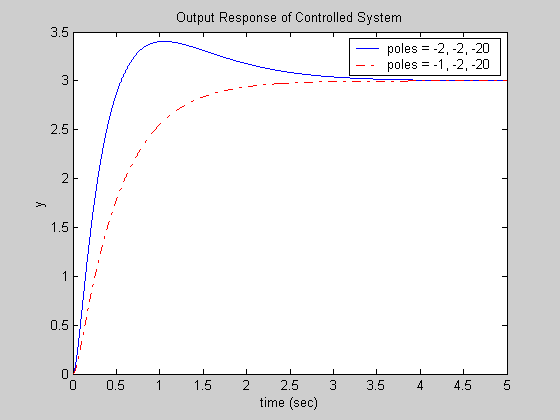
title('Output Response of Controlled System') ;
hold on ;
% Perform Second State Feedback Design
[num,den] = ss2tf(A,B,C,[0]) ; % find TF for open loop system
printsys(num,den,'s') ;
K = acker(Acl, Bcl, [-1 -2 -20]) % determine feedback gains
x = [0; 0] ; y = C*x ; % initial conditions
inte = 0.0 ;
tvec = 0.0 ; yvec = 0.0 ; i = 1 ; % define vectors for storing outputs
for t = 0.0:dt:5.0, % loop over time for simulation
inte = inte + dt*(y - yd) ; % integral of output error
u = -K*[inte; x] ; % state controller
xdot = A*x + B*u ; % plant dynamics
x = xdot*dt + x ; % euler integrate dynamics
y = C*x ; % output equation
yvec(i) = y ; tvec(i) = t ; % store output & time into vectors
i = i + 1 ; % increment vector index
end ;
plot(tvec, yvec, 'r-.') ; % plot alternative design output
hold off ;
legend('poles = -2, -2, -20', 'poles = -1, -2, -20') ;
Matlab Response:
K = 40.0000 -0.5000 8.0000
num/den = 2 s + 2
-------------
s^2 + 8 s + 5
K = 20.0000 8.5000 7.5000
Matlab Plot Generated:
