M-file:
%
% Filename: example1.m
%
% Description: This m-file demonstrates how to
% 1) define and display transfer function and state-space
% model representations,
% 2) plot step responses of systems represented
% in either state-space or transfer function form, and
% 3) convert between state-space and transfer function
% representations.
%
% The DC gearmotor model developed in class is used as
% the example system.
clear; close all; % Clear workspace and close all figures
% Motor parameters:
Jm = 0.01; bm = 0.3; Kt = 0.8;
Ke = 0.8; Ra = 1.4; La = 0.004;
% Gear paramters:
N1 = 10; N2 = 61;
% Load parameters:
Jl = 11; bl = 27;
% Equivalent load seen by motor:
Jt = Jm + (N1/N2)^2*Jl;
bt = bm + (N1/N2)^2*bl;
% State-Space/Variable model definition:
A = [-Ra/La 0 -Ke/La; ...
0 0 1 ; ...
Kt/Jt 0 -bt/Jt];
B = [1/La; 0; 0];
C = [0 0 1];
D = [0];
disp('State-Space Representation by Definition:');
printsys(A, B, C, D);
% Transfer Function model (motor speed)/(armature voltage)
% definition:
numH = Kt; % define numerator and denominator polynomials
denH = conv([La Ra],[Jt bt]) + [0 0 Ke*Kt];
numH = numH/denH(1); % divide numerator and denominator by coefficient
denH = denH/denH(1); % of highest power of s in denominator
disp('Transfer Function by Definition: Omega(s)/Va(s)=');
printsys(numH,denH,'s');
% Determine Transfer Function from State-Space Model using
% built in Matlab function:
[numH2, denH2] = ss2tf(A, B, C, D);
disp('TF from SS via Matlab function: Omega(s)/Va(s)=');
printsys(numH2,denH2,'s');
% Compute State-Space Model from Transfer Function using
% built in Matlab function:
[A2, B2, C2, D2] = tf2ss(numH, denH);
disp('SS from TF via Matlab function:');
printsys(A2, B2, C2, D2);
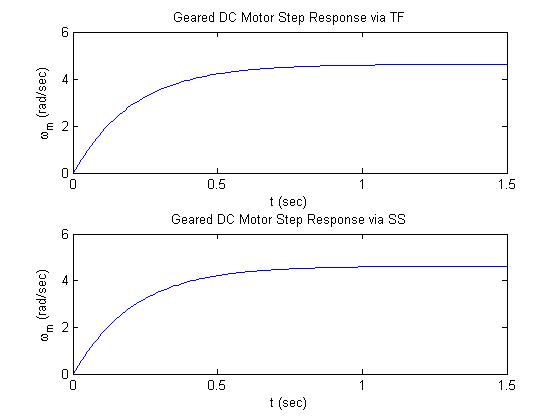
% Plot motor speed response to a 12V step input
ss_sys = ss(A,B,C,D); % create Matlab ss object
tf_sys = tf(numH,denH); % create Matlab tf object
t = 0:0.01:1.5; % define times for step response
[thetamdottf] = 12*step(tf_sys, t); % find step response using tf
subplot(2,1,1); plot(t, thetamdottf); % plot step response
xlabel('t (sec)'); ylabel('\omega_m (rad/sec)');
title('Geared DC Motor Step Response via TF');
[thetamdotss] = 12*step(ss_sys, t); % find step response using ss
subplot(2,1,2); plot(t, thetamdotss); % plot step response
xlabel('t (sec)'); ylabel('\omega_m (rad/sec)');
title('Geared DC Motor Step Response via SS');
Results:
State-Space Representation by Definition:
a =
x1 x2 x3
x1 -350.00000 0 -200.00000
x2 0 0 1.00000
x3 2.61763 0 -3.35584
b =
u1
x1 250.00000
x2 0
x3 0
c =
x1 x2 x3
y1 0 0 1.00000
d =
u1
y1 0
Transfer Function by Definition: Omega(s)/Va(s)=
num/den =
654.4086
----------------------------
s^2 + 353.3558 s + 1698.0725
TF from SS via Matlab function: Omega(s)/Va(s)=
num/den =
654.4086 s
--------------------------------
s^3 + 353.3558 s^2 + 1698.0725 s
SS from TF via Matlab function:
a =
x1 x2
x1 -353.35584 -1698.07248
x2 1.00000 0
b =
u1
x1 1.00000
x2 0
c =
x1 x2
y1 0 654.40860
d =
u1
y1 0
Plots:
